이 글에 제시된 풀이에 오류가 있을 수 있음을 미리 안내드립니다. 오류를 발견하실 시, 댓글로 알려주시면 감사하겠습니다.
문제

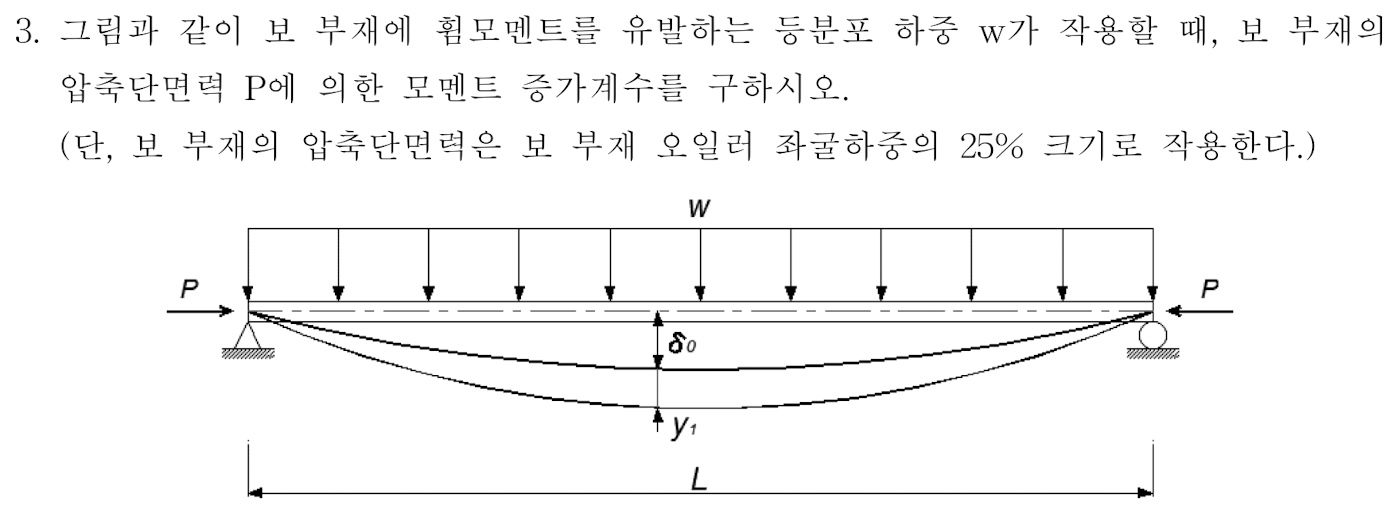
보-기둥 부재에 압축력이 작용할 때, 모멘트 증가계수를 구하는 문제입니다.
풀이

풀이 전 생각
모멘트 확대계수를 역학 문제에서 처음 접해 당황했습니다. 강구조나 철근 콘크리트에서 자주 다루는 내용이지만요.
그래도 모멘트 확대계수의 의미에 따라 유도하면 답이 나올 것이라고 생각했습니다.
처짐 방정식
모멘트 확대계수는 “P-델타 비선형 효과를 고려한 2차 모멘트 / 탄성해석한 1차 모멘트”입니다.
초기 처짐을 y0, 하중에 의한 처짐을 y1으로 두었습니다.
두 처짐의 최대치는 기하학적 형상에 따라 중앙에서 발생하며, 경계조건을 알기 때문에 각 처짐에 대한 미분방정식을 desolve로 풀었습니다.
최대 처짐 및 최대 모멘트
최대 처짐은 중앙에서 발생하며, 변형 후 최대 처짐에 P를 곱한 값이 P-델타 효과(2차 효과)를 고려한 모멘트입니다.
1차 효과 모멘트는 초기 최대 처짐에 를 곱한 값입니다.
모멘트 확대 계수
따라서 모멘트 확대계수는 “기하학적 비선형 효과를 고려한 최대 처짐 / 초기 최대 처짐”입니다.
이를 정리하면 우리가 익숙한 공식으로 나타낼 수 있습니다.
문제에서 하중이 좌굴하중의 0.25라고 주어졌으므로, 값 대입하면 모멘트 확대계수를 구할 수 있습니다.


https://www.slideserve.com/vielka-salas/beam-columns
위 사이트에서 더 자세한 풀이 과정을 확인할 수 있습니다.
난이도
★★★☆☆ (난이도 5점 만점 중 3점)
역학에서 자주 다루지 않는 “P-델타 효과”이지만, 압축재 설계 파트의 개념을 적용하면 어렵지 않습니다.
추가 보충: P-델타 효과, 모멘트 확대 계수
P-델타 효과는 구조물이 횡변위와 축력을 동시에 받을 때 발생하는 추가적인 모멘트를 의미합니다. 이 효과는 특히 고층 구조물 설계에서 반드시 고려해야 합니다.

P-델타 효과의 분류
- P-δ (빅 델타, 부재 효과): 부재의 국부적 변형으로 발생하는 모멘트 증폭입니다. 작은 변형이라도 축력에 의해 모멘트가 증폭되며, 가늘고 긴 부재에서 뚜렷하게 나타납니다.
- P-Δ (스몰 델타, 구조 효과): 건물 전체 변위가 발생했을 때 발생하는 추가 모멘트입니다. 구조물이 휘어질수록 안정성에 큰 영향을 미칩니다.
모멘트 확대계수 (B1, B2)
P-델타 효과를 고려하는 대표적인 방법은 모멘트 확대계수를 사용하는 것입니다. 이를 통해 1차 해석 결과에 비선형 2차 효과를 반영할 수 있습니다.
- B1 계수는 부재의 국부적 변형을 반영하며, 모멘트 감소계수 Cm을 포함하여 비대칭 모멘트 분포를 고려합니다.

- B2 계수는 구조물 전체의 변형을 반영하며, 모멘트골조에 적용됩니다.

모멘트 감소계수 Cm
모멘트 감소계수 Cm는 비대칭 모멘트 분포를 반영하여 실제 모멘트를 감소시키는 역할을 합니다. 이를 통해 부재의 모멘트 불균형을 해결할 수 있습니다.

피-델타 효과 유튜브
피-델타 효과에 대해서도 잘 설명해주신 분이 계시더라고요. 참고하시면 좋을 것 같아 링크를 함께 올립니다.